GAYA ANGKAT (LIFT) DAN GAYA HAMBAT (DRAG)

                                                                                                               by: dodi suroto

PERSAMAAN KONTINYUNITAS DAN PRINSIP BERNOULLI

                                                                                                                  by: dodi suroto

ATMOSPHERE

                                          by: dodi suroto

LIFT AUGMENTATION DEVICES

by: dodi suroto

Lift Augmentation Devices 

The wing of an aircraft is designed for high or cruise speed where lift is mainly created by forward speed only. For slow flight we need to increase lift somehow, but there are limits to what can be done by increasing the angle of attack. Aerodynamicists have devised other ways of increasing the amount of lift generated. These are called lift augmentation devices. Pilots use these devices on almost every flight.

There are several devices that can be used on an aircraft wing to increase the lift. We all know them as leading and trailing edge flaps. Other techniques are also used to increase the angle of attack (coefficient lift): vortex generators, wing fences and discontinuous leading edges.

We will look at these devices on this page, exploring them and seeing how they operate.

Increasing Lift

An aircraft wing, designed for high or cruise speed, can be characterized by having low camber, low thickness/chord (T/C) ratio and you will see the maximum thickness somewhere in the middle of the chord. C_L and drag will also be low compared to high lift wings.

To be able to fly and maneuver safely at low airspeeds the wing must have a high lift aerofoil (high camber, T/C ratio and maximum thickness well forward).

Flaps

All these seemingly conflicting wing properties can be incorporated into one design. To accomplish this, the wing designer uses leading and trailing edge flaps. When deployed, these devices change certain properties of the wing: camber, wing area, etc.

If we revisit the lift formula: L = 1/2 ρ V² x S x C_L, we can see that we have several ways to increase the lift for a given wing. Speed (V), wing area (S) and the coefficient lift (C_L) can be varied for given angle of attack (AOA) to change lift. The use of flaps will change the wing area and coefficient lift.

Flaps

General Aviation aircraft normally use the plain flap, although some manufacturers (Dyn Aero) use the fowler flap on their aircraft. The image shows the types of flaps in use today. From top to bottom: the simple or plain flap, slotted flap, split and fowler flap.

Fowler flaps

Its easy to see that the fowler flap not only increases camber of the wing but also the wing area by moving toward the back, when they are deployed. They have the greatest increase in C_L with the lowest increase in drag, hence the use on high performance aircraft, airliners and so on.

Aerodynamic effects of flaps

The use of trailing edge flaps (lowering them) will have a number of effects aerodynamically. C_L increases for all angle of attacks (AOA), reducing stall speed, results in a higher C_D (with more drag airspeed stabilizes easily), rearward movement of the center of pressure (C_P), a lower stalling AOA, aircraft are more maneuverable and can land at lower speeds resulting in shorter landing distances.

Lift/Drag

Lift/drag ratio (L/D) is also reduced when full flaps are extended. Normally, flap settings between 0 - 25° will noticeably increase lift more than drag, ideal for take off. Flap settings beyond 25° will increase drag much more than lift, ideal for landing and steep approaches.

Flaps also increase the camber and wing area of the wing where they are installed, usually the inner part toward the wing root.

AIRCRAFT STABILITY

                                                                                                   by: dodi suroto

Aircraft Stability 

When an airplane is in straight-and-level flight at a constant velocity, all the forces acting on the airplane are in equilibrium. If that straight-and-level flight is disrupted by a disturbance in the air, such as wake turbulence, the airplane might pitch up or down, yaw left or right, or go into a roll. If the airplane has what is characterized as stability, once the disturbance goes away, the airplane will return to a state of equilibrium.

Static Stability

The initial response that an airplane displays after its equilibrium is disrupted is referred to as its static stability. If the static stability is positive, the airplane will tend to return to its original position after the disruptive force is removed. If the static stability is negative, the airplane will continue to move away from its original position after the disruptive force is removed. If an airplane with negative static stability has the nose pitch up because of wake turbulence, the tendency will be for the nose to continue to pitch up even after the turbulence goes away. If an airplane tends to remain in a displaced position after the force is removed, but does not continue to move toward even greater displacement, its static stability is described as being neutral.

Dynamic Stability

The dynamic stability of an airplane involves the amount of time it takes for it to react to its static stability after it has been displaced from a condition of equilibrium. Dynamic stability involves the oscillations that typically occur as the airplane tries to return to its original position or attitude. Even though an airplane may have positive static stability, it may have dynamic stability which is positive, neutral, or negative.

Imagine that an airplane in straight-and-level flight is disturbed and pitches nose up. If the airplane has positive static stability, the nose will pitch back down after the disturbance is removed. If it immediately returns to straight-and-level flight, it is also said to have positive dynamic stability. The airplane, however, may pass through level flight and remain pitched down, and then continue the recovery process by pitching back up. This pitching up and then down is known as an oscillation. If the oscillations lessen over time, the airplane is still classified as having positive dynamic stability. If the oscillations increase over time, the airplane is classified as having negative dynamic stability. If the oscillations remain the same over time, the airplane is classified as having neutral dynamic stability. Figure 3-61 shows the concept of dynamic stability. In view A, the displacement from equilibrium goes through three oscillations and then returns to equilibrium. In view B, the displacement from equilibrium is increasing after two oscillations, and will not return to equilibrium. In view C, the displacement from equilibrium is staying the same with each oscillation.

Longitudinal Stability

Longitudinal stability for an airplane involves the tendency for the nose to pitch up or pitch down, rotating around the lateral axis (wingtip to wingtip). If an airplane is longitudinally stable, it will return to a properly trimmed angle of attack after the force that upset its flightpath is removed. The weight and balance of an airplane, which is based on both the design characteristics of the airplane and the way it is loaded, is a major factor in determining longitudinal stability. There is a point on the wing of an airplane, called the center of pressure or center of lift, where all the lifting forces concentrate. In flight, the airplane acts like it is being lifted from or supported by this point. This center of lift runs from wingtip to wingtip. There is also a point on the airplane, called the center of gravity, where the mass or weight of the airplane is concentrated. For an airplane to have good longitudinal stability, the center of gravity is typically located forward of the center of lift. This gives the airplane a nose-down pitching tendency, which is balanced out by the force generated at the horizontal stabilizer and elevator. The center of gravity has limits within which it must fall. If it is too far forward, the forces at the tail might not be able to compensate and it may not be possible to keep the nose of the airplane from pitching down. In Figure 3-62, the center of lift, center of gravity, and center of gravity limits are shown. It can be seen that the center of gravity is not only forward of the center of lift, it is also forward of the center of gravity limit. At the back of the airplane, the elevator trailing edge is deflected upward to create a downward force on the tail, to try and keep the nose of the airplane up. This airplane would be highly unstable longitudinally, especially at low speed when trying to land. It is especially dangerous if the center of gravity is behind the aft limit. The airplane will now have a tendency to pitch nose up, which can lead to the wing stalling and possible loss of control of the airplane.

Lateral Stability

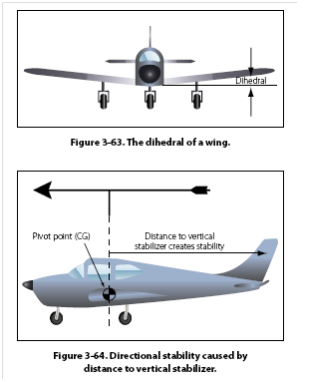
Lateral stability of an airplane takes place around the longitudinal axis, which is from the airplane’s nose to its tail. If one wing is lower than the other, good lateral stability will tend to bring the wings back to a level flight attitude. One design characteristic that tends to give an airplane good lateral stability is called dihedral. Dihedral is an upward angle for the wings with respect to the horizontal, and it is usually just a few degrees. Imagine a low wing airplane with a few degrees of dihedral experiencing a disruption of its flightpath such that the left wing drops. When the left wing drops, this will cause the airplane to experience a sideslip toward the low wing. The sideslip causes the low wing to experience a higher angle of attack, which increases its lift and raises it back to a level flight attitude. The dihedral on a wing is shown in Figure 3-63.

Directional Stability

Movement of the airplane around its vertical axis, and the airplane’s ability to not be adversely affected by a force creating a yaw type of motion, is called directional stability. The vertical fin gives the airplane this stability, causing the airplane to align with the relative wind. In flight, the airplane acts like the weather vane we use around our home to show the direction the wind is blowing. The distance from the pivot point on a weather vane to its tail is greater than the distance from its pivot point to the nose. So when the wind blows, it creates a greater torque force on the tail and forces it to align with the wind. On an airplane, the same is true. With the CG being the pivot point, it is a greater distance from the CG to the vertical stabilizer than it is from the CG to the nose. [Figure 3-64]

Dutch Roll

The dihedral of the wing tries to roll the airplane in the opposite direction of how it is slipping, and the vertical fin will try to yaw the airplane in the direction of the slip. These two events combine in a way that affects lateral and directional stability. If the wing dihedral has the greatest effect, the airplane will have a tendency to experience a Dutch roll. A Dutch roll is a small amount of oscillation around both the longitudinal and vertical axes. Although this condition is not considered dangerous, it can produce an uncomfortable feeling for passengers. Commercial airliners typically have yaw dampers that sense a Dutch roll condition and cancel it out.

NACA Airfoil Series

NACA Airfoil Series

Please send me information on the NACA 4, 5 and 6 digit airfoils. I would like to know some general information, their applications, advantages, disadvantages, and the formulas used to calculate the coordinates.

I'm currently trying to design a 3D model of the B-58 bomber, but I lack the mathematical definitions of NACA profiles such as 0003.46-64.069 (root section) and 0004.08-63 (tip section). I've found 4- and 5-digit NACA airfoil generators, but they don't seem to do the job. Can you provide any help?

As you suggest in your questions, the early NACA airfoil series, the 4-digit, 5-digit, and modified 4-/5-digit, were generated using analytical equations that describe the camber (curvature) of the mean-line (geometric centerline) of the airfoil section as well as the section's thickness distribution along the length of the airfoil. Later families, including the 6-Series, are more complicated shapes derived using theoretical rather than geometrical methods. Before the National Advisory Committee for Aeronautics (NACA) developed these series, airfoil design was rather arbitrary with nothing to guide the designer except past experience with known shapes and experimentation with modifications to those shapes.

This methodology began to change in the early 1930s with the publishing of a NACA report entitled The Characteristics of 78 Related Airfoil Sections from Tests in the Variable Density Wind Tunnel. In this landmark report, the authors noted that there were many similarities between the airfoils that were most successful, and the two primary variables that affect those shapes are the slope of the airfoil mean camber line and the thickness distribution above and below this line. They then presented a series of equations incorporating these two variables that could be used to generate an entire family of related airfoil shapes. As airfoil design became more sophisticated, this basic approach was modified to include additional variables, but these two basic geometrical values remained at the heart of all NACA airfoil series, as illustrated below.

NACA airfoil geometrical construction

NACA Four-Digit Series:

The first family of airfoils designed using this approach became known as the NACA Four-Digit Series. The first digit specifies the maximum camber (m) in percentage of the chord (airfoil length), the second indicates the position of the maximum camber (p) in tenths of chord, and the last two numbers provide the maximum thickness (t) of the airfoil in percentage of chord. For example, the NACA 2415 airfoil has a maximum thickness of 15% with a camber of 2% located 40% back from the airfoil leading edge (or 0.4c). Utilizing these m, p, and t values, we can compute the coordinates for an entire airfoil using the following relationships:

1.      Pick values of x from 0 to the maximum chord c.

2.      Compute the mean camber line coordinates by plugging the values of m and p into the following equations for each of the x coordinates.

3.      Calculate the thickness distribution above (+) and below (-) the mean line by plugging the value of t into the following equation for each of the x coordinates.

4.      Determine the final coordinates for the airfoil upper surface (x_U, y_U) and lower surface (x_L, y_L) using the following relationships.

NACA Five-Digit Series:

The NACA Five-Digit Series uses the same thickness forms as the Four-Digit Series but the mean camber line is defined differently and the naming convention is a bit more complex. The first digit, when multiplied by 3/2, yields the design lift coefficient (c_l) in tenths. The next two digits, when divided by 2, give the position of the maximum camber (p) in tenths of chord. The final two digits again indicate the maximum thickness (t) in percentage of chord. For example, the NACA 23012 has a maximum thickness of 12%, a design lift coefficient of 0.3, and a maximum camber located 15% back from the leading edge. The steps needed to calculate the coordinates of such an airfoil are:

1.      Pick values of x from 0 to the maximum chord c.

2.      Compute the mean camber line coordinates for each x location using the following equations, and since we know p, determine the values of m and k₁ using the table shown below.

3.      Calculate the thickness distribution using the same equation as the Four-Digit Series.

4.      Determine the final coordinates using the same equations as the Four-Digit Series.

Modified NACA Four- and Five-Digit Series:

The airfoil sections you mention for the B-58 bomber are members of the Four-Digit Series, but the names are slightly different as these shapes have been modified. Let us consider the root section, the NACA 0003.46-64.069, as an example. The basic shape is the 0003, a 3% thick airfoil with 0% camber. This shape is a symmetrical airfoil that is identical above and below the mean camber line. The first modification we will consider is the 0003-64. The first digit following the dash refers to the roundedness of the nose. A value of 6 indicates that the nose radius is the same as the original airfoil while a value of 0 indicates a sharp leading edge. Increasing this value specifies an increasingly more rounded nose. The second digit determines the location of maximum thickness in tenths of chord. The default location for all four- and five-digit airfoils is 30% back from the leading edge. In this example, the location of maximum thickness has been moved back to 40% chord. Finally, notice that the 0003.46-64.069 features two sets of digits preceeded by decimals. These merely indicate slight adjustments to the maximum thickness and location thereof. Instead of being 3% thick, this airfoil is 3.46% thick. Instead of the maximum thickness being located at 40% chord, the position on this airfoil is at 40.69% chord. To compute the coordinates for a modified airfoil shape:

1.      Pick values of x from 0 to the maximum chord c.

2.      Compute the mean camber line coordinates using the same equations provided for the Four- or Five-Digit Series as appropriate.

3.      Calculate the thickness distribution above (+) and below (-) the mean line using these equations. The values of the a_x and d_x coefficients are determined from the following table (these are derived for a 20% thick airfoil).

4.      Determine the "final" coordinates using the same equations as the Four-Digit Series.

5.      As noted above, this procedure yields a 20% thick airfoil. To obtain the desired thickness, simply scale the airfoil by multiplying the "final" y coordinates by [t / 0.2].

NACA 1-Series or 16-Series:

Unlike those airfoil families discussed so far, the 1-Series was developed based on airfoil theory rather than on geometrical relationships. By the time these airfoils were designed during the late 1930s, many advances had been made in inverse airfoil design methods. The basic concept behind this design approach is to specify the desired pressure distribution over the airfoil (this distribution dictates the lift characteristics of the shape) and then derive the geometrical shape that produces this pressure distribution. As a result, these airfoils were not generated using some set of analytical expressions like the Four- or Five-Digit Series. The 1-Series airfoils are identified by five digits, as exemplified by the NACA 16-212. The first digit, 1, indicates the series (this series was designed for airfoils with regions of barely supersonic flow). The 6 specifies the location of minimum pressure in tenths of chord, i.e. 60% back from the leading edge in this case. Following a dash, the first digit indicates the design lift coefficient in tenths (0.2) and the final two digits specify the maximum thickness in tenths of chord (12%). Since the 16-XXX airfoils are the only ones that have ever seen much use, this family is often referred to as the 16-Series rather than as a subset of the 1-Series.

NACA 6-Series:

Although NACA experimented with approximate theoretical methods that produced the 2-Series through the 5-Series, none of these approaches was found to accurately produce the desired airfoil behavior. The 6-Series was derived using an improved theoretical method that, like the 1-Series, relied on specifying the desired pressure distribution and employed advanced mathematics to derive the required geometrical shape. The goal of this approach was to design airfoils that maximized the region over which the airflow remains laminar. In so doing, the drag over a small range of lift coefficients can be substantially reduced. The naming convention of the 6-Series is by far the most confusing of any of the families discussed thus far, especially since many different variations exist. One of the more common examples is the NACA 64₁-212, a=0.6.

In this example, 6 denotes the series and indicates that this family is designed for greater laminar flow than the Four- or Five-Digit Series. The second digit, 4, is the location of the minimum pressure in tenths of chord (0.4c). The subscript 1 indicates that low drag is maintained at lift coefficients 0.1 above and below the design lift coefficient (0.2) specified by the first digit after the dash in tenths. The final two digits specify the thickness in percentage of chord, 12%. The fraction specified by a=___ indicates the percentage of the airfoil chord over which the pressure distribution on the airfoil is uniform, 60% chord in this case. If not specified, the quantity is assumed to be 1, or the distribution is constant over the entire airfoil.

NACA 7-Series:

The 7-Series was a further attempt to maximize the regions of laminar flow over an airfoil differentiating the locations of the minimum pressure on the upper and lower surfaces. An example is the NACA 747A315. The 7 denotes the series, the 4 provides the location of the minimum pressure on the upper surface in tenths of chord (40%), and the 7 provides the location of the minimum pressure on the lower surface in tenths of chord (70%). The fourth character, a letter, indicates the thickness distribution and mean line forms used. A series of standaradized forms derived from earlier families are designated by different letters. Again, the fifth digit incidates the design lift coefficient in tenths (0.3) and the final two integers are the airfoil thickness in perecentage of chord (15%).

NACA 8-Series:

A final variation on the 6- and 7-Series methodology was the NACA 8-Series designed for flight at supercritical speeds. Like the earlier airfoils, the goal was to maximize the extent of laminar flow on the upper and lower surfaces independently. The naming convention is very similar to the 7-Series, an example being the NACA 835A216. The 8 designates the series, 3 is the location of minimum pressure on the upper surface in tenths of chord (0.3c), 5 is the location of minimum pressure on the lower surface in tenths of chord (50%), the letter A distinguishes airfoils having different camber or thickness forms, 2 denotes the design lift coefficient in tenths (0.2), and 16 provides the airfoil thickness in percentage of chord (16%).

Further Sources:

This is probably the most theoretical and mathematically-intense answer we have yet given on this site, but let me point out that coordinates for many of these airfoils already exist in print or on the web. In addition, many programs and web sites now exist that can automatically compute the coordinates once the user enters the desired airfoil name or characteristics. Some excellent tools include:

• NACA 4-Digit Series Airfoil Generator
• NACA 5-Digit Series Airfoil Generator
• SNACK -- download this program that includes NACA airfoil coordinate generators for all of the families we have discussed
• XFOIL -- download this airfoil analysis code that includes a 4-Digit and 5-Digit airfoil generation tool, but this program is difficult for a novice to use (program is 100% free)
• UIUC Airfoil Coordinates Database -- vast library of coordinates for many airfoils, including those of the NACA families discussed above
• The Incomplete Guide to Airfoil Usage -- check out the airfoils used on a huge assortment of aircraft

Summary:

Though we have introduced the primary airfoil families developed in the United States before the advent of supersonic flight, we haven't said anything about their uses. So let's briefly explore the advantages, disadvantages, and applications of each of these families.

Family	Advantages	Disadvantages	Applications
4-Digit	1. Good stall characteristics 2. Small center of pressure movement across large speed range 3. Roughness has little effect	1. Low maximum lift coefficient 2. Relatively high drag 3. High pitching moment	1. General aviation 2. Horizontal tails Symmetrical: 3. Supersonic jets 4. Helicopter blades 5. Shrouds 6. Missile/rocket fins
5-Digit	1. Higher maximum lift coefficient 2. Low pitching moment 3. Roughness has little effect	1. Poor stall behavior 2. Relatively high drag	1. General aviation 2. Piston-powered bombers, transports 3. Commuters 4. Business jets
16-Series	1. Avoids low pressure peaks 2. Low drag at high speed	1. Relatively low lift	1. Aircraft propellers 2. Ship propellers
6-Series	1. High maximum lift coefficient 2. Very low drag over a small range of operating conditions 3. Optimized for high speed	1. High drag outside of the optimum range of operating conditions 2. High pitching moment 3. Poor stall behavior 4. Very susceptible to roughness	1. Piston-powered fighters 2. Business jets 3. Jet trainers 4. Supersonic jets
7-Series	1. Very low drag over a small range of operating conditions 2. Low pitching moment	1. Reduced maximum lift coefficient 2. High drag outside of the optimum range of operating conditions 3. Poor stall behavior 4. Very susceptible to roughness	Seldom used
8-Series	Unknown	Unknown	Very seldom used

Today, airfoil design has in many ways returned to an earlier time before the NACA families were created. The computational resources available now allow the designer to quickly design and optimize an airfoil specifically tailored to a particular application rather than making a selection from an existing family. To learn about some more recent developments, check out other questions on supercritical airfoils and airfoil design.